Технически университет – софия

машиностроителен факултет, катедра “прецизна техника и уредостроене”

Лабораторни упражнения по “Метрология и измервателна техника”

ГРЕШКИ И НЕОПРЕДЕЛЕНОСТ НА ИЗМЕРВАНЕТО

Кратка справка по теоретичния материал и процедурите

Грешка на измерване е разликата между резултата от измерване x_изм и истинската x_ист стойност на измерваната величина. Тъй като истинската стойност по природа не може да бъде определена, на практика се използва действителната (приписаната) стойност – най добрата оценка на стойността на величината. Следо-вателно, би могло да се говори за истинска грешка (непознаваема) и действителна грешка (познаваема).

е = x_изм – x_ист .

Очевидно, дименсията на грешката е е еднаква с дименсията на измерваната величина.

Относителна грешка е^* е отношението на грешката на измерване и истинската стойност на измерваната величина. В много случаи тя по-точно може да представи качеството на резултата от измерване.

За оценка на точността на измервателните средства се използва показателят приведена грешка е^о – отношението на грешката и горната граница на обхвата на показанията или интервала на измерване на измервателното средство (най-често, представяно като процент).

6.1. Класификация на грешките

Според проявлението на грешките при повтарящи се измервания, те могат да се разделят на систематични, случайни и груби.

Ø Систематичната грешка има устойчив характер. Тя винаги съпровожда резултата от измерването с постоянна или закономерно променяща се стойност. Числено тя се определя като разлика между средноаритметичната стойност, която би се получила от безкраен брой измервания на една и съща величина, извършени при повтарящи се условия, и истинската стойност на тази величина. По принцип систематичната грешка може да бъде разпозната, определена и резултатът от измерването може да се коригира с нейната стойност.

Ø Случайната грешка характеризира разсейването, т. е. повторяемостта на резултата от единичното измерване. Числено тя се определя като разлика между резултата от измерване и средноаритметичната стойност, която би се получила при безкраен брой измервания на една и съща величина, извършени при повтарящи се условия.

Случайната грешка се дължи на съвместното влияние на различни случайни фактори и нейната стойност не може да бъде определена предварително. По статистически път може да се определи само вероятността за нейното появяване.

Ø Грубата грешка е случайна грешка, чиято стойност рязко се отличава от обик-новено появяващите се грешки. Тя относително лесно може да се разпознае.

Според възможността за корекция грешките могат да се разделят на

¨ Предотвратими. Такива грешки (напр. в резултат от неподходящи условия или неправилно обслужване на измервателните средства) не следва да се допускат. При евентуално появяване те могат да се разпознаят и съответните резултати да не се вземат под внимание (фиг. 6.1.).

¨ Коригируеми. Такава е главната част от систематичните грешки. Тези грешки следва по принцип да се изключат от резултата, освен в случай, че стойностите им са твърде малки в сравнение с другите грешки, или коригирането е много трудоемко. Тогава x_ист = x_изм + Δ_попр. Тук x_ист е коригираният (поправен) резултат, а установената стойност на поправката Δ_попр се прибавя към измерената (непоправена) стойност x_изм.

¨ Некоригируеми са случайните грешки и такива части от систематичните грешки, които с разполагаемите възможности не могат да бъдат разпознати, или пък определянето им е неизгодно по финансови или организационни причини.

Фиг. 6.1. Възможности за коригиране на грешките

Според причината за тяхното появяване грешките могат да се разделят на:

¨ Грешка, породена от принципа или метода на измерване.

¨ Грешка на показанието на измервателното средство (измервателния уред). Тази грешка се дължи на несъвършенства в принципа на действие, конструкцията или изпълнението на уреда и обикновено се определя при зададени (стандартни условия).

¨ Грешка, породена от влияещите величини (фактори). Влиянието на фактори като външната среда (температура, захранващо напрежение, вибрации и пр.), момента на измерването, оператора и т. н. предизвиква допълнителни грешки, които често имат значителна големина в сравнение с грешката на показанието.

Изложеното показва колко е важно да се разбира и отчита разликата между грешката на показанието на измервателното средство и грешката на резултата от измерването.

6.2. Методи за коригиране на систематичните грешки

Внасянето на поправка в резултата от измерването на пръв поглед е лесно, но изучаването на систематичната грешка и определянето на големината й често е сложна и трудоемка задача.

От една страна, нерядко систематичните грешки превишават по големина случайните. От друга – трудностите произтичат от това, че систематичните грешки не могат да се разглеждат обобщено, а изискват специално разглеждане за всяка конкретна измервателна задача.

Могат да се обобщят следните методи за откриване и компенсиране на систематичните грешки.

1. Сравняване на измерените стойности с познати “еталонни” стойности на измерваната величина. Като еталон може да се използва и проверен образец или измервателен уред. Евентуалните поправки на измерваните стойности се представят в таблица или графика.

За да бъде възможно такова сравняване, се поддържа система от еталони и съответни проверочни схеми, позволяващи сравнимост (проследимост) на резултата от измерването с първичния еталон.

2. Оценяване на отклоненията на фактическата функция на преобразуване при измерването x_изх = f(x_вх) спрямо зададената (очакваната) функция. На фиг. 6.2. са показани шест вида типични отклонения на статичните характеристики на измервателните средства спрямо очакваната линейна характеристика.

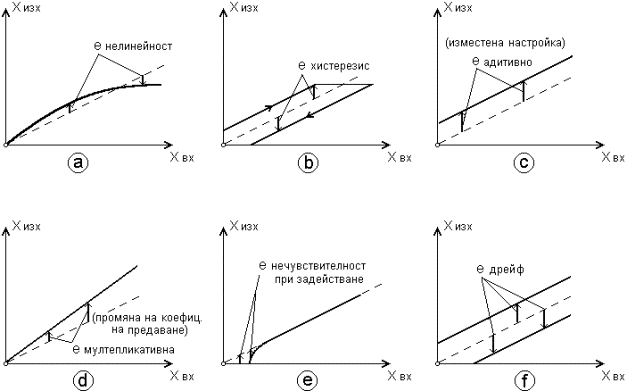
Фиг. 6.2. Систематични отклонения на функцията на преобразуване

Въз основа на оценените отклонения се формират и съответните попоравки.

В тази група следва да се включат и случаите, когато поради характера на метода на измерване, могат да се получават симетрични и противоположни по знак отклонения на резултата от измерването, които взаимно могат да се компенсират.

Такъв случай е например грешката при измерване с кобилична везна поради отклонения на дължината на рамената й, изследвана в настоящото упражнение. Друг пример е грешката при измерване на стъпката на резба с инструментален микроскоп, когато оста на детайла е наклонена спрямо направлението на движение на масата.

3. Оценка на грешките, внасяни от влияещите величини.

Въз основа на установените функционални връзки между тези величини (температура, налягане и пр.) от една страна и съответната грешка на измерване – от друга, се определят стойностите на поправките. Корекцията може да се въведе ръчно (с помощта на съответни таблици или графики) или автоматично, особено при наличие на микропроцесорно устройство в измервателната верига.

6.3. Представяне на случайните грешки

Както бе посочено по-горе, резултатът от измерването, респ. грешката на измерване се формира под влияние на различни систематични и случайни фактори.

При многократно измерване (n пъти) на една и съща величина, непоправените стойности на резултата от измерването x_i¢ се разпределят по нормалния закон (фиг. 6.3.) с център на групиране

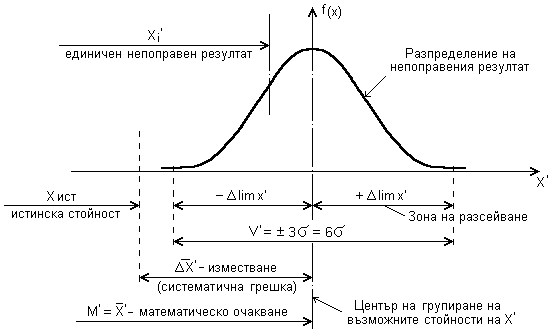
Фиг. 6.3. Разсейване на непоправения резултат от измерването

Зоната на разсейване на възможните стойности на непоправения резул-тат, при доверителна вероятност P = 0,9973 е:

V΄ = ± 3s( x¢) = ± D_lim = 6s( x¢) или

V΄ = ± 3S( x¢) = ± D_lim = 6S( x¢) ,

където S( x¢) е оценката на средноквадратичното отклонение s( x¢) , а

D_lim – граничната случайна грешка.

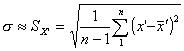Тук центърът на групиране е отместен спрямо истинската стойност x_ист на измерваната величина с отместването , което представлява систематичната грешка на измерването.

След разпознаване на систематичната грешка и определяне на големината й, резултатът от измерването следва да бъде поправен. Разпределението на поправените стойности x_i добива вида, показан на фиг. 6.4.

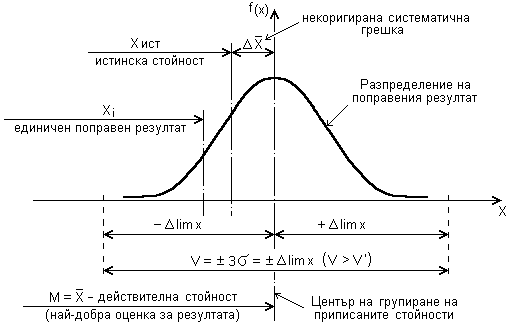
Фиг. 6.4. Разсейване на поправения резултат от измерването

Приема се, че действителната стойност на резултата от измерване, т.е. неговата най-добра оценка, е равна на математическото очакване или сред-ноаритметичната стойност на поправените резултати x_i от единичните измервания.

Действителната стойност на резултата се различава от истинската стойност на измерваната величина със стойността на неразпознатата или некоригирана систематична грешка.

Зоната на разсейване V на възможните стойности x_i на поправения резултат в общия случай се различава от зоната на разсейване V΄ на непоправения резултат x_i¢, тъй като поради непълното познаване на внесените поправки, неизучените систематични грешки се разглеждат като случайни въздействия (рандомизирани систематични грешки).

Трябва специално да се подчертае, че представените по-горе грешки – систематични или случайни, трябва да се разглеждат като конкретни стойности за съответното измерване.

Граничната грешка D_lim, респ. зоната на разсейване V, следва да се разглежда като интервал, в който грешката може да се появи с определена (доверителна) вероятност.

Неопределеност на резултата от измерване

Представянето на резултата от измерване чрез грешката на измерване е ефективно, когато е налице еталон, или друг източник, представящ с известна точност истинската стойност на измерваната величина, а с това – и възможност за оценка на грешката.

При липса на информация за истинската стойност на величината, нейната оценка в процеса на измерване може да бъде направена само с точност до големината на един интервал, в който с определена достоверност може да се очаква, че ще се появи истинската стойност – интервал на неопределеността на резултата.

В последните години международно бе утвърдената методика за оценяване на неопределеността на резултата от измерване. Тя създава възможност за прилагане на унифицирана процедура и достигане до единство при оценка на качеството на получения резултат.

Неопределеност (несигурност) на измерване е параметър, свързан с резултата от измерване, който характеризира дисперсията на стойностите, които могат да бъдат приписани на измерваната величина.

Такъв параметър може да бъде средноквадратичната неопределеност u(x).

u(x) = S(x),.респ. s(x).

Най-често резултатът се представя чрез разширената неопределеност U(x) – полуширината на интервал, в който се преценява, че се намира истинската стойност на измерваната величина.

U(x) = k. u(x).

Коефициентът k, се нарича коефициент на покриване. Обикновено k = 2.

Примери за представяне на резултата от измерване:

x = 5,75 mm U = 0,05, k = 2;

x = 5.75 ± U = 5.75 ± 0.05 mm, k = 2.

В общия случай неопределеността на измерването обхваща много съставящи. Тяхното определяне може да се направи по два пътя.

¨ Оценка тип А. Съставящите, респ. неопределеността се оценяват на базата на статистически анализ на резултатите от серии измервания и се характеризират от експерименталните средноквадратични отклонения.

¨ Оценка тип Б. Средноквадратичната неопределеност се основава на цялата налична информация, получена от:

· данни от предишни измервания;

· опит и общи познания за съответното измерване и измервателно средство;

· сертификати, справочни данни, спецификации на производителите и т.н.

6.4. Сумарна грешка и неопределеност на резултата от измерване (съставяне на бюджет на неопределеността)

Сумарната грешка на резултата от измерване включва компонентите на грешката, генерирани от различните фактори при измерването. По-важните от тях са:

Основна грешка на измервателното средство (ИС). Както посочихме, това е грешката на показанието, получена при нормирани условия.

Грешки, предизвикани от влияещите фактори, в т.ч.:

· От настройката на ИС, вкл. от настроечните мерки;

· От температурата, влажността, налягането;

· От захранващото напрежение, осветеността и пр.;

· От измервателния натиск;

· От ориентацията на детайла и ИС;

· От отклоненията на формата на детайла, грапавостта и т.н.;

· Субективни грешки.

На практика, всяка от компонентите на грешката има и систематична и случайна съставка и може да се представи с разпределението, показано на фиг. 6.3.

Естествено, за разпознатите и оценени систематични грешки трябва да се направи корекция на резултата, поради което по-нататък следва да се разглеждат само случайните и рандомизираните систематични грешки, представени чрез граничните грешки (виж фиг. 6.4.), предизвикани от отделните фактори.

Сумарната граничната грешка се получава въз основа на теоремата за сумиране на дисперсиите:

където са граничните грешки, предизвикани от отделните фактори.

Комбинираната (сумарната) средноквадратична неопределеност u_c(y) на резултата от измерване, когато този резултат е получен в резултат на влиянието на определен брой други величини, е равна на положителния квадратен корен на сумата от дисперсиите на тези величини, претеглени с коефициентите на влияние на тези величини.

При взаимнонезависими (некорелирани) входни величини

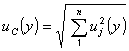
Величината u_j(y) ( j = 1…N ) е приносът на средноквадратичната неопре-деленост на входната величина x_j в средноквадратичната неопределеност на резултата от измерването

u_j(y) = C_j. u(x_j),

където C_j е коефициентът на влияние.

В общия случай интервалът, характеризиращ неопределеността не е иден-тичен на доверителен интервал, свързан с известна доверителна вероятност, особено при включването и на рандомизирани систематични компоненти на грешката.

Бюджет на неопределеността е обобщено представяне на оценяването на съставящите на неопределеността на резултата от измерването. Бюджетът включва списък на всички източници на неопределеност, свързаната с тях средноквадратична неопределеност и методите за нейното оценяване.

6.5. Грешка и неопределеност на резултата от косвени измервания

При косвени измервания търсената величина се определя след измерване на други величини, въз основа на известна функционалната връзка между търсената и входните величини, т.е. y = f (x₁, x₂….x_N).

Ако с D(y), съответно D(x_j), означим систематичните грешки или поправките на търсената и входните величини, връзката между тях, след разлагане в ред на Тейлор и прости преобразувания се определя от уравнението

Тук частните производни представляват коефициентите на влияние на величините x_j. C_j = , (j = 1, 2 …N).

Въз основа на теоремата за сумиране на дисперсиите за комбинираната неопределеност се получава:

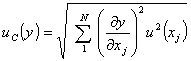Разширената комбинирана неопределеност ще бъде:

U_c(y) = k. u_c(y).